공부전략을 대학교때의 전략으로 바꾸기로 했다.
수업시간에 최대한 머릿속에 입력을 하고,
기초를 따로 채워나가면서 수업시간에 배운내용을 매꿔나가는 것이다.
이렇게 하니깐 멘탈이 회복되면서 지식을 쌓는 느낌이 들었다.
# 그라디언트 디센트
손실함수의 편미분을 구해서 빼주는 방식으로 최저 손실을 만드는 파라미터를 찾아주는것이 그라디언트 디센트였다.
1차 미분을 진행하기 때문에, 국소적으로 봤을때 좋은 로컬 미니멈을 찾아간다.
# 최적화의 컨셉(대부분이 통계학에서 나온 용어들이다.)
Generalization
Under-fitting vs over-fitting
Cross validation
Bias-variance tradeoff
Bootstrapping
Bagging and boosting
# Generalization
일반화성능을 높이는 것이 우리의 목표이다.
그렇다면 일반화 성능이 뭘까?
일반화성능을 높이는 것이 무조건 좋은걸까?
일반화가 무엇인지 알아보자.
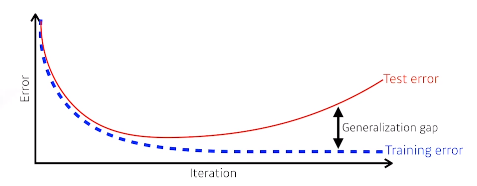
일반적으로 학습을 하게 되면, 학습이 반복됨에 따라 학습데이터에 대한 training error가 줄어들게 된다.
그러나 training error가 줄었들었다고해서 성능이 좋아지는것은 아닌데,
학습에 사용하지 않은 테스트 데이터에 대해서는 성능이 떨어지게 된다.
이것은 test error 라고 하며, 성능 좋은 상태의 training error와 성능이 떨어지게 된 상태의 test error와의 차이를
Generalization gap이라고 한다.
네트워크의 성능이 좋은 generalization을 갖고 있다 라고 한다면, 학습데이터와 비슷하게 나올거라는 보장을 해주는 것이다.
네트워크가 좋지 않아서 학습데이터 성능조차도 좋지 않다면 당연하게도 generalization 성능이 좋다고 해서 test의 데이터의 성능이 좋다고 할 수 없을 것이다.
# underfitting vs overfitting

일반적으로 학습데이터에 잘 동작하지만 테스트데이터에 잘 동작하지 않는 것을 overfitting이라고 한다.
overfitting일 경우엔 학습데이터에 대해서는 대부분 맞추고 있는데, 테스트 데이터에 잘 동작하지 않는다.
네트워크가 너무 간단하거나 트레이닝을 너무 조금 시켜서, 학습데이터조차도 잘 못맞추는것을 underfitting이라고 한다.
이 둘 사이의 balanced가 가장 좋은 것이다.
근데 사실 이건 개념적인 이야기인게, 사실 모델을 만들고자 하는 사람의 맘이다.
모델을 만드는 사람이 모델을 overfitting 된 것을 만들고 싶다면 그냥 그렇게 하면되기 때문이다.
# cross validation

일반적으로 트레이닝 데이터와 테스트 데이터를 나눠서 주는 경우가 많다.
그렇다면 트레이닝 데이터와 테스트 데이터는 얼만큼으로 나눠서 사용하는 것이 좋을까?
예를 들면 절반만 학습하고 절반으로 validation해도 좋을까?
근데 학습량이 너무 적어지는것일수도 있기에 문제가 될 수 있다.
k fold validation이라고 불리기도 하는, 학습데이터를 k개로 나눠서 만약 전체 5개중에 1, 2, 3, 4 번을 학습하고 5번째를 validation에 사용했다면, 두번째 학습때는 1, 2, 3, 5번을 학습하고 4번을 validation으로 사용하는 것이다.
이렇게 validation하는 것을 cross validation이라고 한다.
인공신경망을 학습하는데 있어서 굉장히 많은 하이퍼 파라미터가 존재한다.
일반적으로 파라미터라고 하면 내가 최적화해서 찾고싶어하는 값이다.
convolution filter의 값이라던가, material perception weight와 bias의 값들을 우리가 파라미터라고 부르고,
하이퍼파라미터는 내가 정하는 값이다. 학습률이라던지 네트워크를 얼마나 크게 가져갈지, 어떤 loss 함수를 사용할지.
근데 이런것은 정답이 없으므로, cross validation을 해서 최적의 하이퍼파라미터 값을 찾고
그 다음에 하이퍼 파라미터를 고정한 상태에서 모든 데이터를 다 사용하여 학습한다.
그래야 더 많은 데이터를 가지고 학습할 수 있기 때문이다.
테스트데이터는 학습과정에서 어떤 방법으로든 사용되면 안된다.
학습에는 무조건 train 데이터와 validation 데이터를 사용해야 하고, 테스트 데이터는 절대 사용하면 안된다.
# bias and variance

variance라는것은 어떤 입력을 넣었을때 출력이 얼마나 일관적인가를 나타낸다.
variance가 낮은 모델들은 간단한 모델들이다.
그에 반해서 큰 모델은 비슷한 입력이 들어와도 출력이 많이 달라진다.
이렇게 되면 overfitting 될 가능성이 커질 것이다.
bias는 분산이 좀 되더라도 평균적으로 봤을때 true target에 접근하게 되면 그 자체로 bias가 낮다고 하고,
bias가 높다는 것은 내가 원하고자 하는 true target에서 좀 멀어지게 된다는 것을 의미한다.
# Bias-variance tradeoff
학습데이터에 노이즈가 껴있다고 가정을 했을때,
내가 이 노이즈가 껴있는 데이터를 2 norm 기준으로 최소화 하는 것은 3가지 파트로 나뉠수 있다.
내가 minimize하는것은 한가지 값인데, 이 값이 사실은 3가지 파트로 나눠져 있어서,
하나가 줄면 다른것들은 커질 수 밖에 없다는 트레이드 오프를 말하는 것이다.

t라는게 타겟이고, f햇은 뉴럴 네트워크의 출력이다.
타겟에 노이즈가 있다고 가정하자.
const를 minimize한다는 것은 bias제곱, variance, noise 세가지를 최소화 하는것과 같은 것이다.
즉, 이상적으로 bias와 variance를 줄일수 있는 방법은 기본적으로 존재하기 힘들다는것이다.
# bootstrapping
통계학에서 많이 사용하는 말인데, 신발끈을 묶어서 하늘을 날겠다는 말이다.
학습데이터를 100개가 있으면 그중에 몇개만 활용한 모델을 여러개 만들어서,
하나의 입력에 대해서 모델들이 다른 결과를 보일수 있다.
하나의 입력에 대해서 다른 모델들이 얼마나 일치된 결과를 보이는지 보고,
전체적인 모델의 언썰턴트를 예측하고자 할 때 사용하게 된다.
학습데이터가 고정되어 있을때, 그 학습데이터 안에서 서브샘플링을 해서 여러 모델이나 메트릭을 만들어서 무언가를 하겠다는 것이다.
# bagging vs boosting

bagging(boostrapping aggregating)
모든 학습데이터를 사용해서 한개를 학습하는것이 아니라 학습데이터를 여러개를 만들어서 여러개의 모델을 random subsampling을 통해서 만들고 여러 모델들을 가지고 아웃풋이 나와서 그 아웃풋의 평균을 내겠다는 것이다.
앙상블이라고 불리기도 한다.
근데 이게 재밌는게, 학습데이터를 전부 사용해서 학습하는것이 결과가 좋을것 같지만 사실은 그렇지 않다는 것이다.
캐글같은데서 주로 앙상블을 사용하는 경우가 많은데, 이때 배깅을 주로 사용한다.
boosting
학습데이터가 100개가 있다면 시퀀셜하게 바라보고 모델하나를 간단하게 만들고 학습데이터에 대해서 학습을 하는데,
80개의 데이터가 잘되고 20개의 데이터는 잘 안될 수 있다.
그럼 다른 모델 하나를 더 만들어서 20개의 데이터에 대해서만 잘 동작하는 모델을 만드는 것이다.
이렇게 여러개의 모델을 만들어서 합치는 것이다.
독립적인 모델들이 서로 힘을 합치는 것이 아니라, 하나 하나의 모델들을 시퀀셜하게 합쳐서 하나의 강한 모델을 만드는 것이다.
둘 모두 여러개의 모델을 만들지만 배깅은 독립적인 모델들을 조합하는 것이고, 부스팅은 모델들을 시퀀셜하게 조합해서 하나의 모델처럼 사용하는 것이다.
# gradient descent methods
그라디언트 디센트 메소드를 궂이 분류하자면 3가지로 분류할 수 있다.
stochastic gradient descent : 한번에 한개의 샘플만 보게해서 그라디언트를 구하고 업데이트 한다.
minibatch gradient descent : 한개의 배치만큼의 샘플만 사용해서 그라디언트를 구하고 업데이트 한다.
batch gradient descent : 한번에 모든 데이터의 그라디언트를 구하고 한번에 모든 그라디언트의 평균을 구해서 업데이트 하겠다는 것이다.
일반적인 딥러닝에서는 minibatch를 활용하게 된다.
# batch size matters
배치사이즈라는게 중요하지않은 파라미터라고 볼수 있지만,
한개를 작은 값으로 사용하자고하면 시간이 너무 오래걸리고,
너무 많은 양을 사용하자고하면 네트워크 gpu가 터져버린다.
사실은 배치사이즈가 굉장히 중요하다.
엄청나게 큰 배치를 사용하게 되면 sharp minimize에 도달하게 되고,
작은 배치를 사용하게 되면 flat minimize에 도달하게 된다.

우리는 트레이닝 데이터에 대해서 잘 동작하는 것이 아니라 테스팅 데이터에 대해 잘 동작하는 함수를 원한다.
근데 flat minimum의 특징은 traning function에서 조금 멀어져도 testing function에서도 적당히 낮은 값이 나온다.
트레이닝 데이터에서 잘되면 테스트 데이터에서도 어느정도 잘 된다는 것이다.
즉, generalization performance가 높은 것이다.
sharp minimum 같은 경우는 traning function에서 로컬 미니멈이 되는 값에 도달을 했어도,
tesing function에서 약간만 멀어지게 되면 testring function에서는 가장 높은 값이 나온다.
트레이닝 데이터에서 얻어지는 값들이 테스팅 데이터에서 잘 안될 수 있다는 것이다.
즉, generalization performance가 떨어진다.
논문에서 말하고자 싶은것은 배치사이즈가 작아지게 되면 generalization performance가 좋아진다는 것을 실험적으로 보이고, large 배치사이즈를 어떻게 활용하면 좋을지에 대한 테크닉들을 보여준다.
# gradient descent methods
다양한 방법중에 어찌되었든 하나의 방법을 골라야 한다.
stochastic gradient descent
momentum
nesterov accelarated gradient
adagrad
adadelta
rmsprop
adam
# gradient descent

W는 뉴럴 네트워크의 웨이트를 말한다.
딥러닝 프레임워크는 gradient를 자동으로 계산해주고,
학습률만큼 곱해서 빼주면 업데이트가 된다.
가장 기본적인 방법이지만 문제가 있다면, 학습률이 너무 높으면 학습이 잘못되고 학습률이 너무 작으면 너무 많은 시간이 걸리거나 학습의 효율이 떨어진다.
# momentum

한번 모멘텀이 얻어지면 그것을 계속 이어가자는 것이다.
미니배치를 사용해서 어떤 모멘텀을 얻었다면, 다음 배치에서도 그것을 활용해보자는 것이다.
베타라고 불리는 하이퍼파라미터가 들어간다.
g라고 불리는 그래디언트가 현재 들어왔다면, 다음번 t+1에서는 그래디언트 정보를 버려버리고,
g t+1을 사용하는것이아니라, a t+1이라고 불리는 모멘텀이 그 값을 계속 들고있는 것이다.
모멘텀과 현재 그래디언트를 합친, 모멘텀이 포함된 그래디언트로 업데이트를 시키는 것이다.
이것의 장점은 한번 정해진 그래디언트 방향을 어느정도 유지시켜주기 때문에,
그래디언트가 굉장히 왔다갔다해도, 어느정도 잘 학습되는 효과가 있게 된다.
# nesterov accelerated gradient

nag는 a라고 불리우는 acumulated 그라디언트가 결국 그라디언트 디센트를 하는것인데,
그라디언트를 계산할때 lookahead gradient를 계산한다.
원래 모멘텀은 현재 주어진 그라디언트에서 모멘텀을 acummulaion 했는데,
얘는 한번 이동하고나서 그 간곳에서의 그라디언트를 계산한 것을 가지고 acummulate하는 것이다.

이게 어떤 효과가 있냐면, 일반적으로 모멘텀을 관성이라고 해석하면, 모멘텀을 사용하면 로컬 미니멈을 지나서 슬로프 반대편으로 이동할 수 있다. 그러면 올라갔다가 내려갔다가를 반복하게 되는데, 로컬 미니멈으로 들어가지 못하는 상황이 생긴다.
이에 반해서 nag는 한번 지나간 점에서 그라디언트를 계산하기 때문에 그때 바로 로컬미니멈쪽으로 내려가는 효과가 생기게 된다.
이론적으로 계산하면 conversion rate가 빠르다는 것을 증명할수도 있다.
# adagrad

위에서의 모멘텀을 사용했던 방법과는 달리 adaptive라는 방법들이 있는데, 그 시작이 adagrad이다.
이때부터는 뉴럴네트워크의 파라미터가 얼마나 많이 변해왔는지, 안변해왔는지를 보게된다.
많이 변한 파라미터에 대해서는 더 적게 변화시키고
안변한 파라미터에 대해서는 더 많이 변화시키고 싶어하는 것이다.
그럼 지금까지 파라미터가 얼마나 변했는지에 대한 정보를 저장해야 하는데, 그 값이 G이다.
G는 지금까지 파라미터가 얼마나 변했는지에 대해 제곱해서 더한값이다.
이것을 역수에 넣었기 때문에 많이 변한 파라미터에 대해서는 적게 변화시키고,
적게 변화시키는 파라미터는 많이 변화시키겠다는 것이다.
입실론은 0으로 나눠줄때를 대비해서 넣는것이다.
가장 큰 문제는 G가 계속해서 커지게때문에 무한대로 발산하고 결국에는 항 자체가 0이 되기 때문에 뒤로 가면 갈수록 학습이 멈춰지는 현상이 생기는 것이다.
이런 문제를 해결하고자 하는 방법론들이 뒤에 이어지게 된다.
# adadelta

G가 계속 커지는 것을 해결하겠다는 것인데, 일정시간동안의 윈도우를 만들어서 G를 계산한 다음에 보겠다는 것이다.
문제는 윈도우 사이즈만큼 이전 G정보를 들고있어야 한다.
파라미터가 1000억개라고할때 각각 100개씩 들고있다면 엄청난양의 파라미터를 들고있어야 하고 gpu가 터져버릴 것이다.
이것을 막을 수 있는 방법이 exponential moving average이다.
모두 들고있지 않고 평균값만 들고있으면서 이것을 조금씩 업데이트해주면 100개씩이 아니라 한개만 들고있으면 되기 때문이다.
특징은 학습률이 없다는것인데, 이건 학습자가 바꿀수 있는 요소가 없다는 것을 의미한다.
그래서 많이 활용되지는 않는다.
# RMSprop

논문에 나온것은 아니고 강의하다가 제안하면서 나온 내용이다.
G를 그냥 더하는 것이 아니라, exponential moving average를 사용해서 더해준다.
이것을 분모에다 넣어주고, 네타라는 스텝 사이즈를 넣어준다.
이게 다이고 간단한데 생각보다 성능이 좋았다.
# Adam(adaptive moment estimation)

일반적으로 가장 잘되고 무난하게 사용하는 방법이다.
G를 exponential moving average를 사용해서 더해주는것과 동시에, 모멘텀을 함께 사용하는 것이다.
그래디언트의 크기가 변함에 따라서, 그래디언트 스퀘어의 크기에 따라서, adaptive하게 그래디언트를 정보를 바꿔주는것과 이전에 사용한 모멘텀을 잘 합친게 아담이 된다.
그래서 m이라는게 모멘텀이 되고, v가 그래디언트 스퀘어 평균이 된다.
이 두개를 섞어주는데 하이퍼 파라미터는 베타1, 모멘텀을 얼마나 유지시킬것인가에 대한것과
베타2, 그래디언트 스퀘어에 대한 ema 정보를 얼마나 유지시킬것인가에 대한것,
입실론, 학습률이 있다.
분수는 전체 방법론이 unbiased estimate가 되기 위해서 수학적으로 증명한 것이다.
실제로는 입실론파라미터를 잘 바꿔주는게 실무에서 중요하다.
# regularization
generalization을 잘 되게 하고 싶은것이다.
학습에 방해되도록 규제를 건다는 것이다.
학습을 방해되도록 하는 목적은 학습데이터에만 잘 작동하는것이 아니라 테스트데이터에도 잘 작동하도록 만들어주는 것이다.
이런것들은 어떤 하나의 도구라고 생각하면 좋은데, 학습시킬때 이런 방법들을 적용해서 잘되는 경우가 많다.
early stopping
parameter norm penalty
data augmentation
noise robustness
label smoothing
dropout
batch normalization
# early stopping

이터레이션이 돌아감에 따라서 트레이닝 에러가 줄게되면 테스팅 에러는 커지게 된다.
그래서 너무 많이 학습하기 전에 멈추는 것이다.
근데 언제 멈출지를 알아낼때 test data를 활용하면 치팅이기 때문에,
validation data를 활용해서 언제 멈출지를 알아내게 된다.
# parameter norm penalty
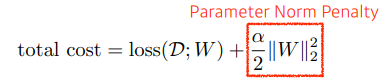
뉴럴네트워크 파라미터가 너무 커지지 않게 하는 것이다.
파라미터들을 모두 제곱한다음에 더해버리면 어떤 값이 나올텐데, 이숫자를 같이 줄이는 것이다.
파라미터들의 절대값을 줄여가자는 것이다.
부드러운 함수일수록 generalization performance가 높을거라고 가정을 하고 진행하는 것이다.
weighted k라고 부르기도 한다.
# Data Augmentation
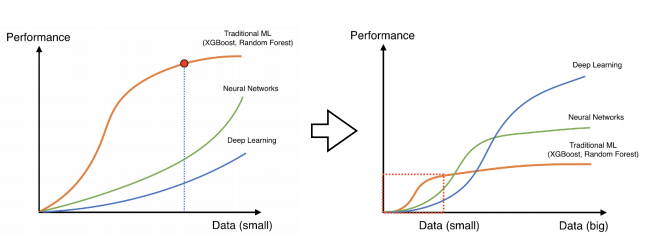
데이터는 다다익선이다.
데이터가 적을때는 기존의 전통적인 기계학습 방법론들이 더 성능이 좋은 경우가 많다.
딥러닝은 데이터가 많을때 더 좋은 성능을 보인다.
데이터를 표현할수 있는 표현력이 더 높은것이다.
그래서 데이터를 지지고 볶아서 데이터를 뿔려서 딥러닝에 사용하는 것이다.

숫자분류를 할때 뒤집는 변환은 막 하면 안된다 6에서 9가 되면 안되기 때문이다.
그러나 다른 이미지 분류 같은경우에서는 뒤집어서 또 학습을 시키는 것이다.
이것을 label preserving augmentation이라고 한다.
이미지를 바꿔서 다른 의미가 된다면 안된다.
# Noise Robustness

이게 왜 잘되는지에 대해서는 말이 많지만 결과적으로는 잘된다.
노이즈를 입력에만 집어넣지않고 웨이트에도 집어넣는다.
웨이트를 학습시킬때 흔들어주면 성능이 더 잘 나온다는 실험적인 결과가 있다.
# label smoothing

데이터 두개를 뽑아서 섞어주는 것이다.
분류 문제를 본다고 하면 디시전 바운더리를 찾고 싶을때 이것을 부드럽게 만들어주는 효과가 있다.

라벨과 이미지를 섞어버리고 강아지 0.5, 고양이 0.5를 줘버리는 것이다.
컷아웃은 일정 영역을 아예 빼버리는 것이고,
컷믹스는 섞어줄때 특정 영역을 나눠서 합쳐주는 것이다.
들인 시간 대비 성능을 많이 올릴수 있는 방법들이다.
# dropout
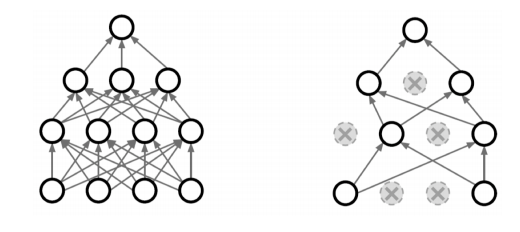
뉴럴 네트워크의 웨이트를 0으로 바꾸는 것이다.
p라는 드랍아웃 ratio를 0.5라면 인퍼런스를 할때에는 뉴런의 50퍼센트를 0으로 바꿔주는것이다.
이렇게 하면 각각의 뉴런들이 더 robust한 feature가 생기게된다고 해석할 수 있다.
일반적으로 성능이 올라가는 효과가 생기게 된다.
# batch normalization

내가 적용하고자하는 레이어에 통계를 정규화 하는것이다.
레이어가 1000개의 파라미터로 되어있는 히든레이어라고 하면
각각의 static를 정규화 시켜주는것이다.
internal feature shift를 줄여서 더 잘 학습된다고 주장하는데, 다른 논문들에서는 동의하지 않는다.
다만 이것은 활용하게 되면, 레이어가 깊을 경우에는 성능이 좋아지게된다.

레이어 전체를 줄이는 경우가 있다면, 인스턴스(이미지 1장)별로 statics를 줄이는 경우도 있고,
그룹별로 줄이는 경우도 있다.
어쨌든 왜 잘되는지 해석하는지보다는 간단한 분류문제에서는 사용하면 성능이 올라가는것으로 알려져 있다.
# 결론
네트워크를 만들고 데이터가 고정되어있고 문제가 고정되어 있을때, 이런 도구들을 넣어보고 genelaization이 잘되는지 확인해가면서 취사선택하면 좋은 결과를 얻게 된다.
# convolution 연산
지금까지의 다층신경망은 각 뉴런들이 선형모델과 활성함수로 모두 연결된 구조였다.
주어진 입력벡터에 대해서 가중치 행렬의 wi 행과 입력 벡터의 내적(행렬곱)을 통해서
잠재변수에 해당하는 변수의 i번째 데이터를 계산할 수있었다.

문제는 hi를 구할때마다 wi가 필요하다는 것이다.
i가 바뀌게 되면 가중치 행렬의 사이즈가 굉장히 커지게 되고, 파라미터의 숫자가 굉장히 많아지게 된다.

convolution 연산은 커널이라는 고정된 가중치 행렬을 사용하고,
고정된 커널을 입력벡터상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조이다.
V에 해당하는것이 커널이고, k가 커널의 사이즈이다.
앞에서 사용된 가중치 행렬과는 조금 다른 사이즈인데,
중요한 것은 입력벡터 X를 모두다 사용하는 것이 아니라,
커널 사이즈 k에 대응되는 사이즈만큼만 입력벡터에서 사용하게 된다.
hi의 값을 계산할때 커널은 그대로 유지하게 되고,
x라는 입력벡터상에서 커널 사이즈만큼 움직여가면서 계산해가는 방식이 convolution연산의 특징이라고 할 수 있다.
i가 바뀌게 되어서 계산을 다시 해야 할때, 활성화 함수와 커널을 제외하고 x입력 벡터 위에서 커널 사이즈 만큼 움직여 가면서 적용된다.
커널을 사용해서 사용하는것도 선형변환의 한 종류에 속하긴 한다.
대신 중요한 것은 가중치 행렬의 i에 따라서 바뀌는 것이 아니라 고정된 커널을 입력벡터위에서 움직여가면서 사용한다는 것이 특징이다.
커널을 공통된 것을 사용하기때문에 가중치 행이 존재하지 않고,
i사이즈와는 상관없이 커널의 크기는 유지되므로 파라미터수를 획기적으로 줄일 수 있게 된다.
# convolution 연산 이해하기

연속인 공간에서 적분을 사용해서 구할수 있고,
이산공간에서는 급수로 표현해서 구한다.
두개인 함수 f와 g가 있을때, x라는 입력에 대해서 계산할때
전체 정의역에 대해서 f와 g에 대해서 z를 움직여가면서 각각 두 함수를 곱해주고 적분을 해주고 더해주는 것이다.
이것은 신호에 해당하는 g와 커널에 해당하는 f에 대해서 구성된다.
(x-z가 들어있거나 i-a가 들어있는 경우가 주로 신호텀,
z만 들어있거나 a만 들어있는 텀이 커널텀이라고 보면된다.)
수학적인 의미는 신호를 커널을 이용하여 국소적으로 증폭 또는 감소시켜서 정보를 추출하거나 필터링 하는 것이다.

엄밀히 말하면 빼기가 아니라 더하기를 사용한 연산을 사용하기 때문에 사실 정확한 용어는 cross-correlation이라고 보는것이 맞다.
하지만 전체공간에서는 이게 플러스인지 마이너스인지 중요하지 않기 때문에, 똑같이 성립하게 된다.
그래서 그냥 역사적으로 convolution이라고 부르는 것이다.
# 그래프적으로 이해하기

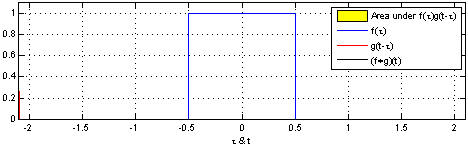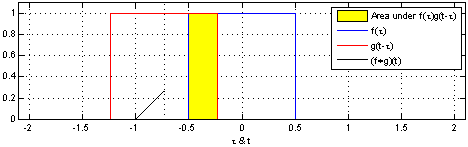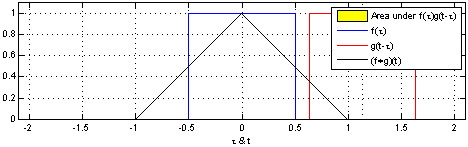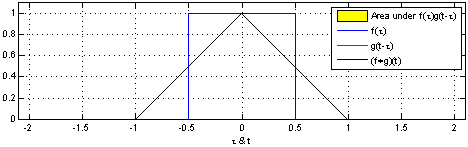

커널은 정의역 내에서 움직여도 변하지 않기 때문에 translation invariant라고 부른다.
주어진 파란색 시그널에 대해서 국소적으로 계산한 결과를 연산을 수행하기때문에 locality가 있다고 하는 것이다.
결과는 검은색으로 나온다.
# 영상처리에서의 convolution



여러가지 커널을 사용할때마다 다른 필터처리한것처럼 다른 영상을 얻을 수 있다.
그래서 영상쪽에서 굉장히 많이 사용하게 된다.
# 더 높은 차원에서의 convolution
앞에서의 연산은 1차원에서의 계산이다.

1차원 컨볼루션은 한 변수에 대해서 움직이고
2차원 컨볼루션은 두 변수에 대해서 동시에 움직인다.
3차원은 3변수이다.
데이터의 성격에 따라 커널의 종류가 달라지기 때문에,
데이터에 따라서 사용방법이 달라지게 된다.
음성이나 텍스트라면 1d를 사용하지만, 흑백이나 칼라, 3d영상이라면 다른것을 사용하게된다.

i, j, k가 변경되어도 커널의 값은 변경되지 않는다는 것을 유념하자.
# 2차원 convolution 연산

행렬모양의 커널을 사용하게 되는데, 2차원에서는 입력위에서 위아래 옆으로 이동하면서 사용한다.

행렬곱이 아니라 성분곱을 해서 더해준다.
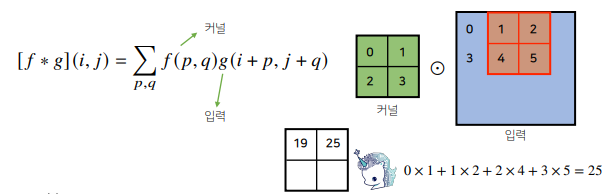
커널을 한칸씩 이동하면서 값을 구한다.
# 출력의 크기

입력이 28이고 커널이 3이면 28 - 3 + 1이므로 결과는 26이된다.
# 3차원 convolution
채널이 여러개인 2차원 입력의 경우 2차원 컨볼루션을 채널 갯수만큼 적용한다고 생각하면된다.

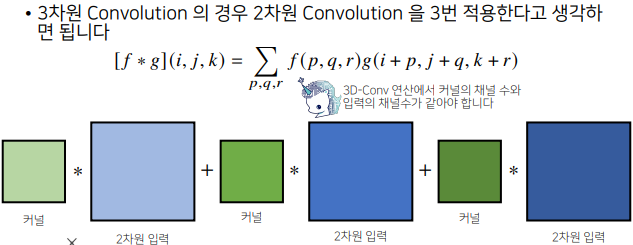
2차원 입력에서 존재하는 채널의 갯수만큼 커널도 그만큼 같은 갯수로 있어야만 2차원 컨볼루션 수행이 가능하다.

커널도 텐서라고 생각하고 적용할 수 있는데,
커널의 채널갯수와 입력의 채널갯수가 같게 설정되고 이 결과들은 연산후에 더해지게 된다.
그래서 출력의 채널은 1이된다.
가로와 출력의 크기는 위에서의 공식으로 얻으면 된다.
# 출력을 여러개 가지게 하려면?

커널 텐서의 갯수를 늘리면 된다.
출력의 차원을 Oc개 만큼 만들고 싶다면,
커널의 갯수를 Oc개 사용하면되는것이다.
즉, 커널을 Oc개 사용하면 출력도 텐서가 된다.
이 방법이 요즘 사용되는 2d이미지에서의 기본적인 방법이고 자주 사용된다.
# convolution 연산의 역전파
역전파를 계산할때도 똑같이 convolution 연산이 수행된다.

convolution 연산에 미분을 해도 똑같이 convolution이 나온다.
이것은 이산데이터에도 똑같이 적용된다.
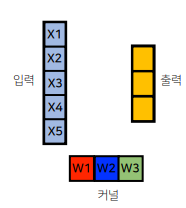
입력의 차원이 5개이고 커널의 차원이 3개면 출력벡터의 차원은 5-3+1이니까 3이된다.


역전파 단계로 돌입하면, 출력벡터의 미분값이 전달된다.



하나의 입력에 대해서 커널이 계산된다고 생각하면 위와 같다.

모든 입력들에 대해서 커널들은 하나로 합쳐지게 된다.
결국은 백워드도 포워드 convolution연산과 같은 것이다.
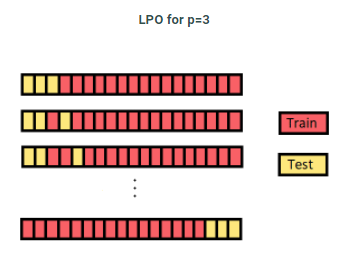
# cross-validation 방법들
Leave p out cross-validation
import numpy as np
from sklearn.model_selection import LeavePOut
data = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6])
lpo = LeavePOut(p=2)
for train, validate in lpo.split(data):
print("Train set:{}".format(data[train]), "Test set:{}".format(data[validate]))Leave one out cross-validation

import numpy as np
from sklearn.model_selection import LeavePOut
data = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6])
lpo = LeavePOut(p=2)
for train, validate in lpo.split(data):
print("Train set:{}".format(data[train]), "Test set:{}".format(data[validate]))Holdout cross-validation

import numpy as np
from sklearn.model_selection import train_test_split
data = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
train, test = train_test_split(data, test_size=0.3, random_state=43)
print('Train:', train, 'Test:', test)k-fold cross-validation

import numpy as np
from sklearn.model_selection import KFold
data = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
kf = KFold(n_splits=3)
for train, test in kf.split(data):
print('Train{}'.format(data[train]), 'Test{}'.format(data[test]))Stratified k-fold cross-validation
위에서 논의한 모든 교차 검증 기술의 경우 불균형 데이터 세트에서 제대로 작동하지 않을 수 있습니다. 계층화 된 k- 겹 교차 검증은 불균형 데이터 세트의 문제를 해결했습니다.
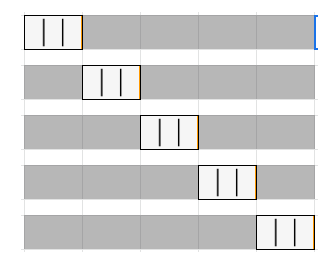
계층화 된 k- 겹 교차 검증에서 데이터 세트는 검증 데이터가 동일한 수의 대상 클래스 레이블 인스턴스를 갖도록 k 그룹 또는 접기로 분할됩니다. 이렇게하면 특히 데이터 세트가 불균형 인 경우 하나의 특정 클래스가 유효성 검사 또는 학습 데이터에 과도하게 존재하지 않습니다.
import numpy as np
from sklearn.model_selection import StratifiedKFold
data = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6])
y = np.array([1,1,1,1,1,0])
skf = StratifiedKFold(n_splits = 2, shuffle=True)
for train, validate in skf.split(data, y):
print('Tran:', data[train], 'Test:', data[validate])
MONTE CARLO, Repeated random subsampling validation

from sklearn.model_selection import ShuffleSplit
import numpy as np
data = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
shuffle = ShuffleSplit(n_splits=5, test_size=0.2, random_state=42)
for train, validate in shuffle.split(data):
print('Train:', data[train], 'Test:', data[validate])
Time Series cross-validation

# Time series의 경우 일반적인 k-fold cv를 사용해도 될까요?
안된다, 시계열 데이터를 처리할때는 두가지 이유때문에 기존 교차 검증을 사용할 수없다.
1. 시간적 종속성
시계열 데이터의 경우 데이터 유출을 방지하기 위해 데이터를 분할 할 때 특히 주의해야 한다.
2. 테스트 세트의 임의 선택
테스트 세트의 선택은 상당히 임의적이고, 그 선택은 테스트 세트 오류가 독립적인 테스트 세트에 대한 잘못된 추정치이다. 따라서 Nested Cross-Validation 를 사용해야 한다.

'ai tech' 카테고리의 다른 글
| ai tech 14일차 (0) | 2021.02.04 |
|---|---|
| ai tech 13일차 (0) | 2021.02.03 |
| ai tech 11일차 (0) | 2021.02.01 |
| ai tech 10일차 (0) | 2021.01.29 |
| ai tech 9일차 (0) | 2021.01.28 |