벌써 10일차에 돌입했다. 슬슬 적응되어가니 속도좀 내어볼까?
matplotlib
# 개론
우리의 데이터는 어떻게 생겼을까?
파이썬의 데이터 시각화 도구
다양한 그래프를 지원하고 판다스와 연동된다.
pyplot이라는 객체를 사용하여 데이터를 표시
객체에 그래프를 쌓은다음 flush하는 개념이다.
import matplotlib.pyplot as plt
X = range(100)
Y = range(100)
plt.plot(X, Y)
plt.show()최대 단점 argument를 kwargs로 받는다
그래서 알트탭으로 어떤 데이터를 받는지 확인이 어렵다.
# figure 객체
그래프는 원래 figure객체에 생성된다.
pyplot객체를 사용하면, 기본 figure에 그래프가 그려진다.
X_1 = range(100)
Y_1 = [np.cos(value) for value in X]
X_2 = range(100)
Y_2 = [np.sin(value) for value in X]
plt.plot(X_1, Y_1)
plt.plot(X_2, Y_2)
plt.show()matplotlib는 figure안에 axes로 구성된다.
figure위에 여러개의 axes를 생성한다.

즉, plot()메서드로 하나하나 쌓아서 show()메소드로 한번에 보여준다고 생각하면된다.
# figure 설정
fig = plt.figure() # figure 반환
fig.set_size_inches(10, 5) # 크기 지정
ax_1 = fig.add_subplot(1, 2, 1) # 두개의 plot 생성
ax_2 = fig.add_subplot(1, 2 ,2) # 두개의 plot 생성
ax_1.plot(X_1, Y_1, c="b")
ax_2.plot(X_2, Y_2, c="g")
plot.show() # show and flush
# subplot
subplot(행 갯수, 열 갯수, 그릴그래프)
fig = plt.figure()
fig.set_size_inches(5, 5)
# plt.stylel.use("ggplot")
ax = []
colors = ["b", "g", "r", "c", "m", "y", "k"]
for i in rnage(1, 7):
ax.append(fig.add_subplot(2, 3, i))
X_1 = np.arange(50)
Y_1 = np.random.read(50)
c = colors[np.random.randint(1, len(colors))]
ax[i-1].plot(X_1, Y_1, c=c)
# set color
color 속성을 사용
흑백, rgb color, predefined color 사용 가능
plt.plot(X_1, Y_1, color="#eeefff")
plt.plot(X_2, Y_2, color="r")
plt.show()# line style
plt.plot(X_1, Y_1, c="b", linestyle="dashed")
plt.plot(X_2, Y_2, c="r", ls="dashdot")
plt.show()
# set title
플롯 위에 title을 작성할 수 있다.
plt.plot(X_1, Y_1, color="b", linestyle="dashed")
plt.plot(X_2, Y_2, color="r", linestyle="dotted")
plt.title("Two lines")
plt.show()제목에는 latex 타입의 표현도 가능하다
plt.title('$y = \\frac{ax + b}{test}$')
plt.show()# legend, 범례
plt.plot(X_1, Y_1, color="b", linestyle="dashed", label="line_1")
plt.plot(X_2, Y_2, color="r", linestyle="dotted", label="line_2")
plt.legend(shadow=True, fancybox=True, loc="lower right")
# set grid & xylim
보조선을 그리고 xy축 범위의 한계를 지정할 수 있다.
plt.grid(True, lw=0.4, ls="--", c=".90")
plt.xlim(-100, 200)
plt.ylim(-200, 200)
# ggplot
plt.style.use("ggplot") # 스타일 적용
plt.plot(X_1, Y_1, color="b", linestyle="dashed")
plt.plot(X_2, Y_2, color="r", linestyle="dotted")
plt.title("$y = \\frac{ax + b}{test}$")
plt.show()
# save
plt.savefig("test.png", c="a")
plt.show()# scatter(산점도)
data_1 = np.random.rand(512, 2)
data_2 = np.random.rand(512, 2)
plt.scatter(data_1[:,0], data_1[:,1], c="b", marker="x")
plt.scatter(data_2[:,0], data_2[:,1], c="r", marker="^")
plt.show()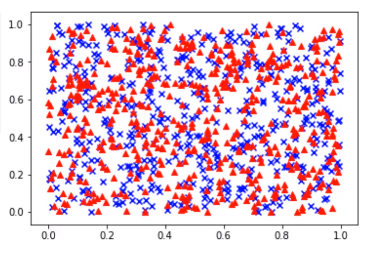
표시할 데이터의 크기를 지정하여 데이터의 크기비교가 가능하다.
N = 50
x = np.random.rand(N)
y = np.random.rand(N)
colors = np.random.rand(N)
area = np.pi * (15 * np.random.rand(N)) ** 2
plt.scatter(x, y, s=area, c=colors, alpha=0.5)
plt.show()
# bar chart
data = [
[5., 25., 50., 20.],
[4., 23., 51., 17.],
[6., 22., 52., 19.]
]
X = np.arange(4)
plt.bar(X + 0.00, data[0], color="b", width=0.25)
plt.bar(X + 0.25, data[1], color="g", width=0.25)
plt.bar(X + 0.50, data[2], color="r", width=0.25)
plt.xticks(X+0.25, ("A", "B", "C", "D"))
plt.show()
color_list = ['b', 'g', 'r']
data_label = ["A", "B", "C"]
X = np.arange(data.shape[1])
for i in range(data.shape[0]):
plt.bar(X, data[i], bottom=np.sum(data[:i], axis=0), color=color_list[i], label=data_label[i])
plt.legent()
plt.show()
A = [5.0, 30.0, 45.0, 22.0]
B = [5, 25, 50, 20]
X = range(4)
plt.bar(X, A, color="b")
plt.bar(X, B, color="r", bottom=60)
plt.show()
women_pop = np.array([5, 30, 45, 22])
men_pop = np.array([5, 25, 50, 20])
X = np.arange(4)
plt.barh(X, women_pop, color="r")
plt.barh(X, -men_pop, color="b")
plt.show()
# histogram
X = np.random.randn(1000)
plt.hist(X, bins=100)
plt.show()
# boxplot
data = np.random.randn(100, 5)
plt.boxplot(data)
plt.show()
전체를 4등분해서 Q1부터 Q3까지를 IQR(interquartile range)라고 한다.
최소값은 왼쪽으로 IQR을 1.5배 한 만큼 그려지고,
최대값을 오른쪽으로 IQR을 1.5배 한 만큼 그려진다.
그리고 그 외 값은 그 바깥에 그려진다.
IQR에 대부분의 데이터가 있다.

# seaborn
matplotlib에 기본 설정을 추가
복잡한 그래프를 간단하게 만들 수 있는 wrapper
간단한코드 + 예쁜결과
lineplot, scatterplot, coutplot 등
import numpy as np
import pandas as pd
import natplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")
tips = sns.load_dataset("tips")
fmri = sns.load_dataset("fmri")
sns.set_style("whitegrid")
sns.lineplot(x="timepoint", y="signal", data=fmri)
카테고리 데이터를 넣어서 구분할 수도 있다.
sns.lineplot(x="timepoint", y="signal", hue="event", data=fmri)
# scatterplot
sns.scatterplot(x="total_bill" y="tip", data=tips)
sns.regplot(x="total_bill", y="tip", data=tips)
sns.scatterplot(x="total_bill", y="tip", hue="time", data=tips)
# countplot
sns.countplot(x="smoker", data=tips)
sns.countplot(x="smoker", hue="time", data=tips)
# barplot
윗부분의 bar는 평균을 의미한다.
bar가 넓으면 분포가 넓다는 것을 의미한다.
sns.barplot(x="day", y="total_bill", data=tips)
sns.barplot(x="day", y="total_bill", data=tips, extimator=np.std)
# distplot
sns.distplot(tips["total_bill"], bins=10, kde=False)
# 그 외의 다양한 plot들
violinplot: boxplot에 distribution을 함께 표현한다.

stripplot: scatter와 category 정보를 함께 표현한다.
swarmplot: 분포와 함께 scatter를 함께 표현한다.

pointplot: category별로 numeric의 평균, 신뢰구간을 표시한다.
regplot: scatter와 선형함수를 함께 표시한다.
catplot: 카테고리 별로 데이터를 보여준다.
facetgrid: 카테고리 데이터를 결합분포로 볼때 사용한다.

# 모수
통계적 모델링은 적절한 가정 위에서 확률 분포를 추정하는 것이 목표이다.
유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아낸다는 것은 불가능하다.
근사적으로 확률분포를 추정할 수 밖에 없다.
예측모형의 목적은 분포를 정확하게 맞추는 것보다는 데이터와 추정방법의 불확실성을 고려해서 위험을 최소화 하는 것이다.
데이터가 어떤 특정한 확률 분포를 따를것이라고 가정한 다음에 그 분포를 결정하는 모수를 추정하는 방법을 모수적 방법론이라고 한다.
특정한 확률분포를 가정하지 않고 데이터에 따라 모델의 구조와 모수의 개수가 유연하게 바뀐다면 비모수 방법론이라고 한다.
비모수방법론이라고 해서 모수가 없다는 것은 아니다.
둘의 차이는 모수가 어떤 분포를 따를것이라고 미리 가정을 하는가 안하는가의 차이이다.
# 확률분포가정하는 예시
우선 히스토 그램을 통해 모양을 관찰한다.
데이터가 2개의 값만 가지는 이분법적인 경우: 베르누이분포
데이터가 n개의 특정한 범위 내에서 값을 가지는 경우: 카테고리분포
데이터가 0과 1사이에서 실수값을 가지는 경우: 베타분포
데이터가 0이상의 값을 가지는 경우: 감마분포, 로그정규분포
데이터가 실수전체에서 값을 가지는 경우: 정규분포, 라플라스분포
하지만, 기계적으로 확률분포를 딱딱 가정해서는 안되고, 데이터를 생성하는 원리를 먼저 알고나서 가정해야 하는것이 원칙이다.
각각의 분포마다 검정하는 방법이 있으므로, 모수를 추정한 후에는 반드시 검정을 해야 한다.
# 데이터로 모수 추정해보기
데이터의 확률분포를 가정했다면 모수를 추정할 수 있다.
정규분포의 모수는 평균과 분산이다.
통계량은 다음과 같다.

표본평균: 주어진 데이터들의 산술평균이다. 표본평균의 기댓값은 모집단의 평균과 기댓값이 일치하게된다.
표본분산: 주어진 데이터에서 표본평균을 빼서 제곱을 한것을 산술평균한 것이다. 표본분산의 기대값은 모집단의 분산기댓값과 일치하게된다.
표본분산을 구할때는 N개가 아니라 N-1개로 나눠서 평균을 구하는데, 불편추정량을 구하기 위해서인데,
표본으로 기댓값을 취했을때, 원래 모집단의 기댓값과 같은 결과를 얻기 위한것이다.
쉽게 생각하면 표본분산을 구하면 어찌되었든 전체에서 일부 분산을 구한것이기 때문에 분산이 모집단보다 적게 나올수밖에 없는데, 이를 보정하기 위해서 N이 아니라 N-1로 나눠주는것이다.
# 중심극한정리
통계량의 확률분포(표본평균과 표본분산의 분포, 표본데이터의 분포가 아니다!)를 표집분포라고 부르는데, 표본평균의 표집분포는 N이 커질수록 정규분포를 따른다. 이것을 중심극한정리라고 부른다.
모집단의 분포가 정규분포를 따르든 따르지 않든 표집분포는 N이 커질수록 정규분포를 따른다.
쉽게 말해서 표본평균과 표본분산을 여러번 구해서 이것을 그래프로 나타내면 정규분포를 따른다는 것이다.
# 최대가능도 추정법
표본평균이나 표분분산은 중요한 통계량이지만 확률분포마다 사용하는 모수가 다르므로, 적절한 통계량이 항상 표본평균이나 표본분산인 것은 아니다.
이론적으로 가장 가능성이 높은 모수를 추정하는 방법중 하나는 최대가능도 추정법(manimum likelihood extimation)이다.
가능도함수는 데이터가 주어져 있는 상황에서 쎄타를 변형시킴에 따라 값이 바뀌는 함수이다.
확률밀도함수에서 모수를 변수로 보는 경우에 이 함수를 가능도함수라고 한다.
모수 쎄타를 따르는 분포가 데이터x를 관찰할 가능성을 뜻하고 확률로 해석하면 안된다.
쉽게 말하면 확률분포곡선에서 특정한 부분의 확률을 계산하는 확률과는 반대로, 가능도에서는 특정한 값이 이미 주어져 있고, 확률 분포곡선자체를 움직이면서 그 값이 가장 잘 나올만한 위치를 찾는것이다.
# 로그가능도
데이터 집합의 행벡터가 독립적으로 추출되었을 경우 로그가능도를 최적화한다.

곱셈이 아니라 덧셈으로 바꿔주기 위해서 로그를 취해주는것이다.
데이터의 숫자가 적으면 상관없지만 만약 데이터의 숫자가 수억단위가 된다면 컴퓨터의 정확도로는 가능도를 계산하는 것이 불가능하다. 컴퓨터는 실수를 정확하게 나타내지 않기 때문에 가령 0에서 1사이의 값을 매우 많이 곱해주면, 그 수를 정확히 나타내는것이 불가능하기 때문이다. 그런데 데이터가 독립이어서 로그를 사용하게 되면 가능도의 곱셈을 로그가능도의 덧셈으로 변경하게 되면 컴퓨터로 연산이 가능해진다.
경사하강법으로 가능도를 최적화하는 경우가 많은데, 이때는 미분을 사용한다.
로그가능도를 사용하면 연산량을 O(n^2)에서 O(n)으로 줄일수있다.
손실함수의 경우 경사하강법을 사용하므로 음의 로그가능도를 최적화하게 된다.
# 최대가능도 추정법 예시
정규분포를 따르는 확률변수 X로부터 독립적인 표본을 얻었을 때 최대 가능도 추정법을 이용하여 모수를 추정하면

정규분포는 평균과 분산을 모수로 가진다.

로그를 취해서 계산하게 되면, 지수를 없애고 뺄셈만으로 이루어진 식을 얻을 수 있는데,
첫번째 식은 분산만으로 이루어져있는식이고, 두번째 식은 분산과 평균으로 이루어진 식을 얻을 수 있다.

첫번째 식과 두번째 식에 대해서 평균으로 미분을 하게되면 분산으로 이루어진 첫번째 식은 사라지고, 오른쪽의 평균으로 이루어진 식만 살아남게 된다.(위에 수식)
첫번째 식과 두번째 식에 대해서 표준편차로 미분을 하게 되면 아래 수식처럼 된다.

최대가능도 추정법을 이용하여 구한 분산은 n-1이 아닌 n으로 나눠주기 때문에 불편추정량을 보장하지 않는다.
# 최대가능도 추정법 예시2
카테고리분포의 경우에는 각각의 차원에서 0또는 1이 될 확률들을 나타낸 분포라고 보면된다.
쉽게 생각하면 주사위를 생각하면되는데 주사위는 1, 2, 3, 4, 5, 6 여섯가지 값중에 한개만 1로 표현되고 나머지는 0으로 표현될 수 있다.

당연하게도 모든 확률을 다 더했을때는 1이 되어야 한다.

로그를 적용해주면 합계로 표현하게 된다.


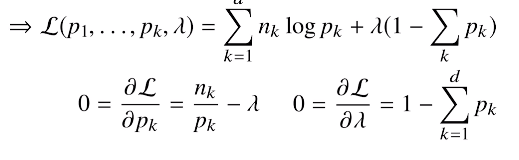

# 딥러닝에서의 최대가능도 추정법
최대가능도 추정법을 이용해서 기계학습 모델을 학습 할 수 있다.

# 확률분포의 거리
기계학습에서의 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 거리를 통해 유도된다.
데이터공간에 두개의 확률분포가 있을 경우 두 확률분포 사이의 거리를 계산 할 때 다음과 같은 함수들을 이용한다.
총변동거리
쿨백-라이블러발산
바슈타인거리
# 쿨백-라이블러발산
분류 문제에서 정답레이블을 P, 모델 예측을 Q라 두면 최대가능도 추정법은 쿨백-라이블러 발산을 최소화 하는것과 같다.

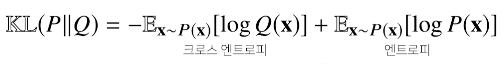
# 확률과 가능도의 차이
개념: 확률은 어떤 모집단의 분포를 통해 어떤 값이 나올 확률을 얻어내는 것이고, 가능도는 일부 표본분포를 통해 모집단의 분포를 추정해내는 것이다.
확률밀도함수에서의 차이: 모집단으로부터의 확률분포를 나타낸것이 확률밀도함수이고, 가능도는 특정한 값이 이미 주어져있을때 확률밀도함수를 움직여 이 값과 최대한 일치하도록 변경하는것이다.
# 확률대신 가능도를 사용하였을때의 이점은 무엇인가?
# 다음의 코드가 나타내는 확률분포는 무엇인가?
쎄타는 무엇을 의마하는가?
import numpy as np
import matplotlib.pyplot as plt
theta = np.arange(0, 1, 0.001)
p = theta ** 3 * (1 - theta) ** 7
plt.plot(theta, p)
plt.show()
'ai tech' 카테고리의 다른 글
| ai tech 12일차 (0) | 2021.02.02 |
|---|---|
| ai tech 11일차 (0) | 2021.02.01 |
| ai tech 9일차 (0) | 2021.01.28 |
| ai tech 8일차 (0) | 2021.01.27 |
| ai tech 7일차 (0) | 2021.01.26 |